Bayesian networks are very well suited to model the statistical relations of genetic material of relatives in a pedigree. They can directly be applied in kinship analysis with any type of pedigree of relatives of the missing persons. An additional advantage of a Bayesian network approach is that it makes the analysis tool more transparent and flexible, allowing to incorporate other factors that play a role such as measurement error probability, missing data, statistics of more advanced genetic markers etc.
The computational engine of Bonaparte uses automatically generated Bayesian networks and Bayesian inference methods, enabling to correctly do kinship analysis on the basis of DNA profiles combined with pedigree information. It is specifically designed to handle large scale incidents with thousands of victims and missing persons.
In the remainder of this section we will describe the Bayesian model approach that has been taken in the development of the application. We formulate the computational task, which is the computation of the likelihood ratio of two hypotheses. The main ingredient is a probabilistic model P of DNA profiles. Before discussing the model, we will first provide a brief introduction to DNA profiles. In the last part of the section we describe how P is modeled as a Bayesian network, and how the likelihood ratio is computed.
Assume we have a pedigree with an individual MP who is missing (the Missing Person). In this pedigree, there are some family members that have provided DNA material, yielding the profiles. Furthermore there is an Unidentified Individual UI, whose DNA is also profiled. The question is, is UI=MP? To proceed, we assume that we have a probabilistic model P for DNA evidence of family members in a pedigree. To compute the probability of this event, we need hypotheses to compare. The common choice is to formulate two hypotheses. The first is the hypothesis H1 that indeed UI=MP. The alternative hypothesis H0 is that UI is an unrelated person U. In both hypotheses we have two pedigrees: the first pedigree has MP and family members FAM as members. The second one has only U as member. To compare the hypotheses, we compute the likelihoods of the evidence from the DNA profiles under the two hypotheses,
Under the model P, the likelihood ratio of the two hypotheses is
If in addition a prior odds P(Hp)=P(Hd)is given, the posterior odds P(Hp|E)=P(Hd|E) follows directly from multiplication of the prior odds and likelihood ratio,
In this subsection we provide a brief introduction on DNA profiles for kinship analysis. A comprehensive treatise can be found in literature. In humans, DNA found in the nucleus of the cell is packed on chromosomes. A normal human cell has 46 chromosomes, which can be organized in 23 pairs. From each pair of chromosomes, one copy is inherited from father and the other copy is inherited from mother. In 22 pairs, chromosomes are homologous, i.e., they have practically the same length and contain in general the same genes ( functional functional elements of DNA). These are called the autosomal chromosomes. The remaining chromosome is the sex-chromosome.Males have an X and a Y chromosome. Females have two X chromosomes.
More than 99% of the DNA of any two humans of the general population is identical. Most DNA is therefore not useful for identification. However, there are well specified locations on chromosomes where there is variation in DNA among individuals. Such a variation is called a genetic marker. In genetics, the specified locations are called loci. A single location is a locus.
In forensic research, the short tandem repeat (STR) markers are currently most used. The reason is that they can be reliable determined from small amounts of body tissue. Another advantage is that they have a low mutation rate, which is important for kinship analysis. STR markers is a class of variations that occur when a pattern of two or more nucleotides is repeated. For example,
The number of repeats x (which is 3 in the example) is the variation among the population. Sometimes, there is a fractional repeat, e.g. CATGCATGCATGCA, this would be encoded with repeat number x =3.2, since there are three repeats and two additional nucleotides. The possible values of x and their frequencies are well documented for the loci used in forensic research. These ranges and frequencies vary between loci. To some extend they vary among subpopulations of humans. The STR loci are more or less standardized. The collection of markers yields the DNA profile. Since chromosomes exist in pairs, a profile will consist of pairs of markers. For example (the following notation is not common standard)
in which each μxs is a number of repeats at a well defined locus m. However, since chromosomes exists in pairs, there will be two alleles μx1 and μx2 for each location, one paternal—on the chromosome inherited from father— and one maternal. Unfortunately, current DNA analysis methods cannot identify the phase of the alleles, i.e., whether an allele is paternal or maternal. This means that (μx1, μx2)cannot be distinguished from (μx2, μx1). In order to make the notation unique, we order the observed alleles of a locus such that μx1 ≤ μx2. Chromosomes are inherited from parents. Each parent passes one copy of each pair of chromosomes to the child. For autosomal chromosomes there is no (known) preference which one is transmitted to the child. There is also no (known) correlation between the transmission of chromosomes from different pairs. Since chromosomes are inherited from parents, alleles are inherited from parents as well. However, there is a small probability that an allele is changed or mutated. This mutation probability is about 0.1%. Finally in the DNA analysis, sometimes failures occur in the DNA analysis method and an allele at a certain locus drops out. In such a case the observation is (μx1;F), in which “F” is a wild card.
In this subsection we will describe the building blocks of a Bayesian network to model probabilities of DNA profiles of individuals in a pedigree. First we observe that inheritance and observation of alleles at different loci are independent. So for each locus we can make an independent model Pμ . In the model description below, we will consider a model for a single locus, and we will suppress the μ dependency for notational convenience.
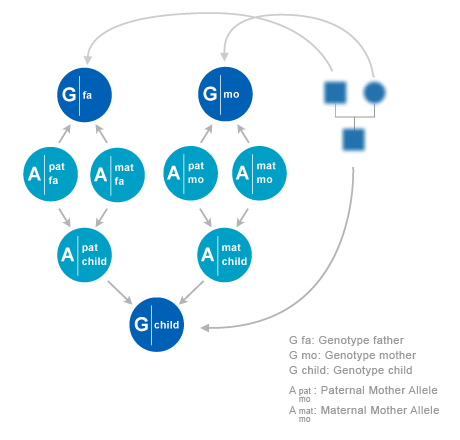
We will consider pedigrees with individuals i. In a pedigree, each individual i has two parents, a father f(i) and a mother m(i). An exception is when a individual is a founder. In that case it has no parents in the pedigree.
Statistical relations between DNA profiles and alleles of family members can be constructed from the pedigree, combined with models for allele transmission. On the given locus, each individual i has a paternal allele xfi and a maternal allele xmi. f and m stands for ‘father’ and ‘mother’. The pair of alleles is denoted as xi =(xfi,xmi). Sometimes we use superscript s which can have values {f,m}. So each allele in the pedigree is indexed by (i,s), where i runs over individuals and s over phases (f,m). The alleles can assume N values, where N as well as the allele values depend on the locus.
An allele from a founder is called ‘founder allele’. So a founder in the pedigree has two founder alleles. The simplest model for founder alleles is to assume that they are independent, and each follow a distribution P(a) of population frequencies. This distribution is assumed to be given. In general P(a) will depend on the locus. More advanced models have been proposed in which founder alleles are correlated. For instance, one could assume that founders in a pedigree come from a single but unknown subpopulation. This model assumption yield corrections to the outcomes in modelswithout correlations between founders. A drawback is that these models may lead to a severe increase in required memory and computation time. In this chapter we will restrict ourself to models with independent founder alleles. If an individual i has its parents in the pedigree the allele distribution of an individual given the alleles of its parents are as follows,
where
To explain in words: individual i obtains its paternal allele xfi from its father f(i). However, there is a 50% chance that this allele is the paternal allele xff(i) of father f(i) and a 50% chance that it is his maternal allele xmf(i).
The probabilities P(xfi|xsf(i)) and
P(xmi|xsm(i)) are given by a mutation model
P(a|b), which encodes the probability that allele of the child is a while the allele
on the parental chromosome that is transmitted is b. The precise mutation mechanisms
for the different STR markers are not known. There is evidence that mutations
from father to child are in general about 10 times as probable as mutations
from mother to child. Gender of each individual is assumed to be known, but for
notational convenience we suppress dependency of parent gender. In general, mutation
tends to decrease with the difference in repeat numbers |a-b|. Mutation is also
locus dependent.
Several mutation models have been proposed in literature. As we will see later, however, the inclusion of a detailed mutation model may lead to a severe increase in required memory and computation time. Since mutations are very rare, one could ask if there is any practical relevance in a detailed mutation model. The simplest mutation model is of course to assume the absence of mutations, P(a|b)=δa,b. Such model enhances efficient inference. However, any mutation in any single locus would lead to a 100% rejection of the match, even if there is a 100% match in the remaining markers. Mutation models are important to get some model tolerance against such case. The simplest non-trivial mutation model is a uniform mutation model with mutation rate m (not to be confused with the locus index μ),
An advantage of this model is that the required memory and computation time increases only slightly compared to the mutation free model. Note that the population frequency is in general not invariant under this model: the mutation makes the frequency more flat. One could argue that this is a realistic property that introduces diversity in the population. In practical applications in the model, however, the same population frequency is assumed to apply to founders in different generations in a pedigree. This implies that if more unobserved references are included in the pedigree to model ancestors of an individual, the likelihood ratio will (slightly) change. In other words, formally equivalent pedigrees will give (slightly) different likelihood ratios.
Observations are denoted as x̄i, or x̄ if we do not refer to an individual. The parental origin of an allele can not be observed, so alleles xf=a, xm=b yields the same observation as xf=b, xm=a. We adopt the convention to write the smallest allele first in the observation: x̄(a,b) ⇔,a ≤ b. In the case of an allele loss, we write x̄ =(x,F)where F stands for a wild card. We assume that the event of an allele loss can be observed (e.g. via the peak height). This event is modeled by L. With L = 1 there is allele loss, and there will be a wild card ?. A full observation is coded as L = 0. The case of loss of two alleles is not modeled, since in that case we simply have no observation. The observation model is now straightforwardly written down. Without allele loss (L = 0), alleles y results in an observation y. This is modeled by the deterministic table
Note that for a given y there is only one x̄ with x̄ = y. With allele loss (L = 1), we have
and
I.e., if one allele is lost, the alleles (a,b) lead to an observation a (then b is lost), or to an observation b (then a is lost). Both events have 50% probability. If both alleles are the same, so the pair is (a,a), then of course a is observed with 100% probability.
By multiplying all allele priors, transmission probabilities and observationmodels, a Bayesian network of alleles x and DNA profiles of individuals x̄ in a given pedigree is obtained. Assume that the pedigree consists of a set of individuals J=1,…,K with a subset of founders F, and assume that allele losses Lj are given, then this probability reads
Under this model the likelihood of a given set DNA profiles can now be computed. If we have observations x̄j from a subset of individuals j ∈ O, the likelihood of the observations in this pedigree is the marginal distribution P({x̄}O), which is the marginal probability
This computation involves the sum over all states of allele pairs xi of all individuals. A junction tree-based algorithm can straightforwardly applied to compute the desired likelihood. In this way, likelihoods and likelihood ratios are computed for all loci, and reported to the user.